Exercícios Resolvidos Enem Raciocínio Lógico.

RACIOCÍNIO LÓGICO.

Lista de questões resolvidas do ENEM sobre Raciocínio Lógico.

(ENEM 2015) Para uma alimentação saudável, recomenda-se ingerir, em relação ao total de calorias diárias, 60% de carboidratos, 10% de proteínas e 30% de gorduras. Uma nutricionista, para melhorar a visualização dessas porcentagens, quer dispor esses dados em um polígono. Ela pode fazer isso em um triângulo equilátero, um losango, um pentágono regular, um hexágono regular ou um octógono regular, desde que o polígono seja dividido em regiões cujas áreas sejam proporcionais às porcentagens mencionadas. Ela desenhou as seguintes figuras:

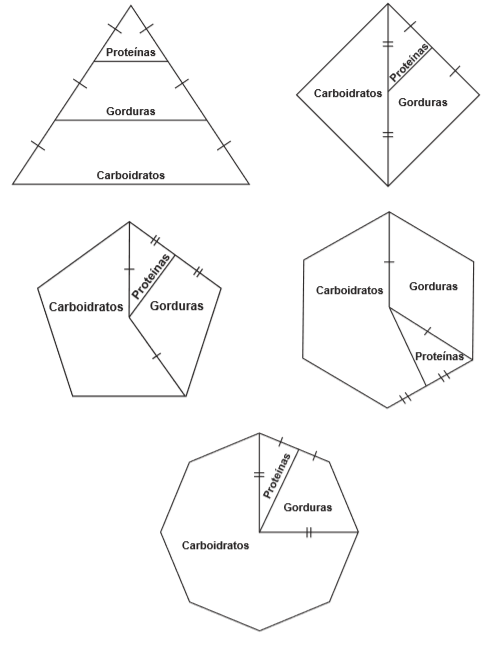
Entre esses polígonos, o único que satisfaz as condições necessárias para representar a ingestão correta de diferentes tipos de alimentos é o

A) triângulo.

B)  losango

C) pentágono.

D) hexágono.

E) octógono.

RESOLUÇÃO

A única figura que pode representar as porcentagens citadas é o pentágono.

O pentágono é formado por 5 triângulos. 

Se o pentágono todo for 100%, então cada triângulo representa 20%. 

Os Carboidratos ocupam três triângulos, logo 3*20% = 60%. 

Proteínas ocupam metade de um  triângulo, logo 20%/2 = 10%, sobrando 30% para Gorduras.

GABARITO B

(ENEM 2015) Em uma central de atendimento, cem pessoas receberam senhas numeradas de 1 até 100. Uma das senhas é sorteada ao acaso.

Qual é a probabilidade de a senha sorteada ser um número de 1 a 20?

a) 1/100

b) 19/100

c) 20/100

d) 21/100

e) 80/100

RESOLUÇÃO

Probabilidade é: O que queremos / Tudo o que temos.

O que queremos são os números de 1 a 20, logo 20 números.

Tudo o que temos são os números 1 a 100, então temos 100 números no total, assim:

A probabilidade será 20/100.

GABARITO C

(ENEM 2015) No contexto da matemática recreativa, utilizando diversos materiais didáticos para motivar seus alunos, uma professora organizou um jogo com um tipo de baralho modificado. No início do jogo, vira-se uma carta do baralho na mesa e cada jogador recebe em mãos nove cartas. Deseja-se formar pares de cartas, sendo a primeira carta a da mesa e a segunda, uma carta na mão do jogador, que tenha um valor equivalente àquele descrito na carta da mesa. O objetivo do jogo é verificar qual jogador consegue o maior número de pares. Iniciado o jogo, a carta virada na mesa e as cartas da mão de um jogador são como no esquema:

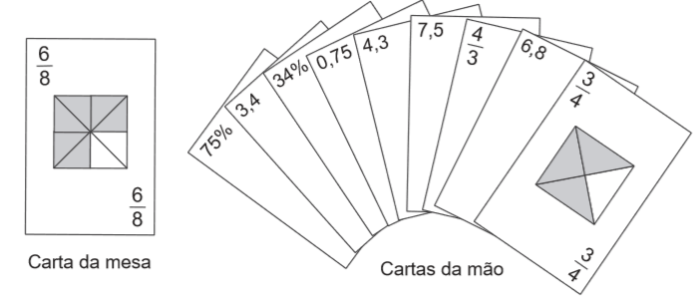
Segundo as regras do jogo, quantas cartas da mão desse jogador podem formar um par com a carta da mesa?

A) 9

B) 7

C) 5

D) 4

E) 3

RESOLUÇÃO

Veja que não temos no baralho nenhuma carta escrita exatamente 6/8, entretanto temos com valores equivalentes.

Simplificando 6/8 temos 3/4, além do mais, 3 dividido por 4 resulta em 0,75 e 0,75 é o mesmo que 75/100 que é o mesmo que 75%.

Logo, temos 3/4; 0,75 e 75%.

GABARITO E.

(ENEM 2015) Após realizar uma pesquisa de mercado, uma operadora de telefonia celular ofereceu aos clientes que utilizavam até 500 ligações ao mês o seguinte plano mensal: um valor fixo de R$ 12,00 para os clientes que fazem até 100 ligações ao mês. Caso o cliente faça mais de 100 ligações, será cobrado um valor adicional de R$ 0,10 por ligação, a partir da 101ª até a 300ª; e caso realize entre 300 e 500 ligações, será cobrado um valor fixo mensal de R$ 32,00.

Com base nos elementos apresentados, o gráfico que melhor representa a relação entre o valor mensal pago nesse plano e o número de ligações feitas é:

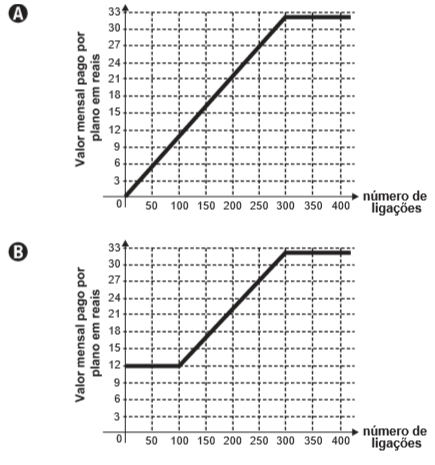
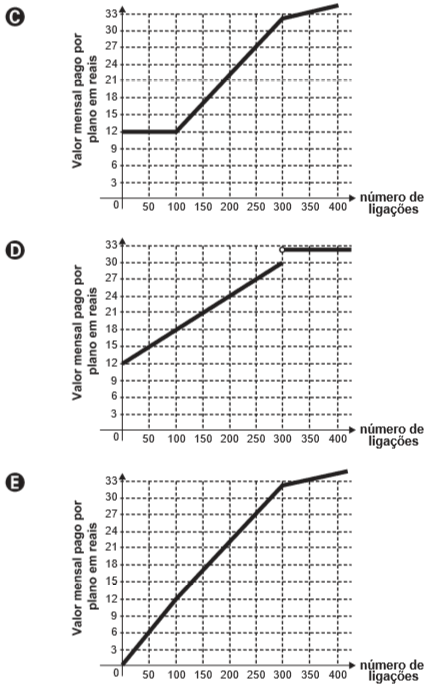
O gráfico certo terá as seguintes informações:

1. Valor de R$ 12,00 constante até 100 ligações;
2. Valores crescentes até a 300ª;
3. Da 300ª até a 500ª o valor será constante de R$ 32,00.

A única alternativa que satisfaz essas condições é B

(ENEM 2015) A insulina é utilizada no tratamento de pacientes com diabetes para o controle glicêmico. Para facilitar sua aplicação, foi desenvolvida uma “caneta” na qual pode ser inserido um refil contendo 3 ml de insulina, como mostra a imagem.

Para controle das aplicações, definiu-se a unidade de insulina como 0,01 mL. Antes de cada aplicação, é necessário descartar 2 unidades de insulina, de forma a retirar possíveis bolhas de ar. A um paciente foram prescritas duas aplicações diárias: 10 unidades de insulina pela manhã e 10 à noite. Qual o número máximo de aplicações por refil que o paciente poderá utilizar com a dosagem prescrita?

A) 25

B) 15

C) 13

D) 12

E) 8

RESOLUÇÃO:

Como antes de cada aplicação deve-se descartar 0,02 ml (2 unidades), então a cada aplicação serão gastos 0,12 ml. Logo, o número máximo de aplicações será:

3 / 0,12 = 25 aplicações.

GABARITO A.