Ele fundamentou a matemática ocidental. Sua obra descreve métodos para resolver equações lineares e quadráticas, como ensinam na escola até hoje. O italiano Fibonacci levou os ensinamentos de Khwarizmi para a Europa, propagando o uso de numerais arábicos e dos algarismos de 0 a 9 para representá-los.
Matemática, Universo e Relações em Cadeia
sexta-feira, 24 de março de 2017
AL-KHWARIZMI - Criou bases teóricas para a álgebra moderna no século 8
AL-KHWARIZMI - Criou bases teóricas para a álgebra moderna no século 8
EUCLIDES - Fundamentou a geometria no século 3 a.C
EUCLIDES - Fundamentou a geometria no século 3 a.C
Seu livro Elementos, com os fundamentos da geometria clássica, ainda é leitura obrigatória entre os matemáticos. Na obra de 23 séculos atrás estão compilados seus axiomas – verdades lógicas que valem até hoje. Um exemplo de axioma é “pode-se traçar uma única reta ligando quaisquer dois pontos”. A obra- prima de Euclides é o segundo livro mais traduzido da história, atrás apenas da Bíblia.
quinta-feira, 23 de março de 2017
HENRI POINCARÉ - Inventou a topologia algébrica no século 19
HENRI POINCARÉ - Inventou a topologia algébrica no século 19
De 1873 a 1875 estudou na Escola Politécnica e em 1875 ingressou na Escola Nacional Superior de Minas (École des Mines). Em 1879 obteve seu doutorado em ciências matemáticas com uma tese sobre equações diferenciais. Seu trabalho foi feito com a orientação de Hermite e fazia parte da banca, Gabriel Darboux, conhecido por seus trabalhos com geometria não-euclidiana.
Em 1881 tornou-se professor na Universidade de Paris, assumindo a cadeira de física matemática, onde permaneceu até sua morte em 17 de julho de 1912.
Durante toda sua vida, Poincaré publicou mais de 500 trabalhos, entre livros e artigos, além de suas notas de aula. Seu pensamento influenciou a matemática, a física matemática e a filosofia, desde a teoria de funções e topologia, até um modo particular de pensar o mundo e sua lógica.
| Jules Henri Poincaré nasceu em 29 de abril de 1854, em Nancy, França, filho de uma família influente na sociedade da época. Seu pai era professor na Universidade de Nancy e o tio, Antoine, engenheiro. Vários membros de sua família tornaram-se conhecidos, tanto na política quanto na vida intelectual da França, principalmente Raymond Poincaré, presidente da França durante a Primeira Guerra Mundial. Suas habilidades matemáticas começaram a ser vistas quando ainda estudava no Liceu de Nancy, ao participar, e vencer, um concurso entre todos os liceus da França, além de se destacar em todas as disciplinas que estudava [GILLISPIE]. |
Em 1881 tornou-se professor na Universidade de Paris, assumindo a cadeira de física matemática, onde permaneceu até sua morte em 17 de julho de 1912.
Durante toda sua vida, Poincaré publicou mais de 500 trabalhos, entre livros e artigos, além de suas notas de aula. Seu pensamento influenciou a matemática, a física matemática e a filosofia, desde a teoria de funções e topologia, até um modo particular de pensar o mundo e sua lógica.
RENÉ DESCARTES - Criou a geometria analítica no século 17
RENÉ DESCARTES - Criou a geometria analítica no século 17
Grande feito dentro da matemática.
Responsável por representar os números naquele gráfico com eixos x e y, batizado de cartesiano em sua homenagem. A geometria analítica revolucionou a matemática, tornando mais fácil “enxergar” relações entre números e compreender conceitos abstratos. Descartes morreu de pneumonia no castelo da rainha Cristina da Suécia, que o contratou como professor de filosofia.
Responsável por representar os números naquele gráfico com eixos x e y, batizado de cartesiano em sua homenagem. A geometria analítica revolucionou a matemática, tornando mais fácil “enxergar” relações entre números e compreender conceitos abstratos. Descartes morreu de pneumonia no castelo da rainha Cristina da Suécia, que o contratou como professor de filosofia.
quinta-feira, 20 de outubro de 2016
Como Aprender Matemática
A matemática é considerada um grande problema para muitos, o aprendizado muitas vezes não acontece devido a diversos fatores, neste texto vamos abordar o que se deve fazer para que se aprenda mais facilmente este conteúdo.
Inicialmente temos que entender que nossa mente sempre tem a capacidade de aprender e que o aprendizado acontece de varias formas.
Uma mente cansada ou esgotada vai estar limita então deve se ter o controle, saber quando e porque você está cansado.
* Escolher o melhor material para aprender matemática é algo muito pessoal e depende do seu propósito de estudo e o seu nível de conhecimento. Escolha um livro-texto que apresenta bastante exemplos resolvidos e relacionam a teoria com aplicações no dia a dia.
* Outra forma que também pode funcionar nos momentos iniciais são as videoaulas, hoje em dia já é possível encontrar vários conteúdos no youtube.
* Escolha um lugar da sua casa para ser o seu ambiente de estudos.
* Procure sempre curtir paginas no face book que tenham como tema o assunto Matemática, se relacionar com amigos estudantes que tenham facilidade no conteúdo também vai te ajudar muito.
* Crie um cronograma semanal com todas as suas atividades e em seguida defina o horário mais adequado para você estudar.
* Resolva os exercícios resolvidos. Nos livros- textos, costuma- se ter exercícios resolvidos. Tente resolvê-los sem olhar a solução. Se tiver dificuldade, veja a parte que está com dificuldade e volte na resolução até conseguir chegar na conclusão sozinho.
O seu aprendizado depende de você, do seu esforço, estaremos sempre aqui para ajudar. Em breve mais dicas aqui no blog.
quarta-feira, 20 de julho de 2016
Exercícios Resolvidos Enem Equações 1º e 2º Graus.
EQUAÇÕES 1º e 2º GRAUS.
Lista de questões resolvidas do ENEM sobre Equações 1º e 2º Graus.
(ENEM 2009) Um grupo de 50 pessoas fez um orçamento inicial para organizar uma festa, que seria dividido entre elas em cotas iguais. Verificou-se ao final que, para arcar com todas as despesas, faltavam R$ 510,00, e que 5 novas pessoas haviam ingressado no grupo. No acerto foi decidido que a despesa total seria dividida em partes iguais pelas 55 pessoas. Quem não havia ainda contribuído pagaria a sua parte, e cada uma das 50 pessoas do grupo inicial deveria contribuir com mais R$ 7,00.
De acordo com essas informações, qual foi o valor da cota calculada no acerto final para cada uma das 55 pessoas?
a) R$ 14,00.
b) R$ 17,00.
c) R$ 22,00.
d) R$ 32,00.
e) R$ 57,00.
Resolução:
De acordo com o enunciado da questão, 50 pessoas já haviam pagado sua parte da despesa total, por isso não consideraremos o valor total para elas, apenas o valor de R$ 7,00 adicional, que deverá ser multiplicado por 50 pessoas. Além desse pessoal, outros cinco juntaram-se ao grupo e precisam pagar sua parte, um valor que não conhecemos e, portanto, podemos identificar como x. Somando-se o valor que essas pessoas pagarão ao valor acrescentado ao restante do grupo, teremos um recolhimento de R$ 510,00. Podemos então montar uma equação do 1° grau:
(50 · 7) + (5 · x) = 510
350 + 5x = 510
5x = 510 – 350
5x = 160
x = 32
Portanto, cada um pagou o valor total de R$ 32,00. Logo, a alternativa correta é a letra d.
(ENEM 2010) O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.
Disponível em: www.cbat.org.br (adaptado).
Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre
a) 4,0 m e 5,0 m.
b) 5,0 m e 6,0 m.
c) 6,0 m e 7,0 m.
d) 7,0 m e 8,0 m.
e) 8,0 m e 9,0 m.
Resolução:
Podemos interpretar o enunciado da questão como:
- No primeiro salto, ele atinge uma distância desconhecida, que pode ser chamada de x m;
- No segundo salto, a distância diminui 1,2 m em relação ao primeiro salto, logo a distância é de(x – 1,2) m;
- No terceiro salto, a distância reduz ainda 1,5 m em relação ao anterior, portanto a distância é(x – 1,2 – 1,5) m, que equivale a (x – 2,7) m.
Se o atleta pretende alcançar a distância total de 17,4 m, somando as distâncias em cada salto, teremos a seguinte equação do 1° grau:
x + (x – 1,2) + (x – 2,7) = 17,4
x + x – 1,2 + x – 2,7 = 17,4
3x – 3,9 = 17,4
3x = 17,4 + 3,9
3x = 21,3
x = 21,3
3
x = 7,1
Portanto, o valor de alcance do primeiro salto é 7,1 m. Esse valor está entre 7,0 m e 8,0 m, sendo assim, a alternativa correta é a letra d.
(ENEM 2010) Uma escola recebeu do governo uma verba de R$ 1000,00 para enviar dois tipos de folhetos pelo correio. O diretor da escola pesquisou que tipos de selos deveriam ser utilizados. Concluiu que, para o primeiro tipo de folheto, bastava um selo de R$ 0,65 enquanto para folhetos do segundo tipo seriam necessários três selos, um de R$ 0,65, um de R$ 0,60 e um de R$ 0,20. O diretor solicitou que se comprassem selos de modo que fossem postados exatamente 500 folhetos do segundo tipo e uma quantidade restante de selos que permitisse o envio do máximo possível de folhetos do primeiro tipo.
Quantos selos de R$ 0,65 foram comprados?
a) 476
b) 675
c) 923
d) 965
e) 1 538
Resolução:
Para que fossem enviados 500 selos do segundo tipo, mais x selos do primeiro tipo, totalizando um valor igual ou inferior a R$ 1000,00, tem-se:
x.(0,65)+500(0,65+060+0,20) ≤ 1000.
x≤423,07. Logo, x=423 selos primeiro tipo.
Assim, o total de selos de R$ 0,65 que foram comprados é de 923.
c) 923
(ENEM 2010) O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.
Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre:
a) 4,0 m e 5,0 m.
b) 5,0 m e 6,0 m.
c) 6,0 m e 7,0 m.
d) 7,0 m e 8,0 m.
e) 8,0 m e 9,0 m.
Resolução:
Sendo x o valor do primeiro salto, (x - 1,2) será o valor do segundo salto e (x – 2,7) o valor do terceiro salto, logo para que o atleta alcance a meta de 17,4m no salto triplo
x + (x- 1,2)+(x - 2,7) terá que ser igual a 17,4, tem-se:
x + (x- 1,2)+(x - 2,7) = 17,4 , x=7,1m.
Logo, considerando os seus estudos, terá que alcançar 7,1m no primeiro salto para atingir a meta de 17,4 m.
d) 7,0 m e 8,0 m.
(ENEM 2009) Um grupo de 50 pessoas fez um orçamento inicial para organizar uma festa, que seria dividido entre elas em cotas iguais. Verificou-se ao final que, para arcar com todas as despesas, faltavam R$ 510,00, e que 5 novas pessoas haviam ingressado no grupo. No acerto foi decidido que a despesa total seria dividida em partes iguais pelas 55 pessoas. Quem não havia ainda contribuído pagaria a sua parte, e cada uma das 50 pessoas do grupo inicial deveria contribuir com mais R$ 7,00.
De acordo com essas informações, qual foi o valor da cota calculada no acerto final para cada uma das 55 pessoas?
a) R$ 14,00.
b) R$ 17,00.
c) R$ 22,00.
d) R$ 32,00.
e) R$ 57,00.
Resolução:
A despesa pode ser escrita de duas formas de acordo com o valor x que será pago por cada uma das 55 pessoas no acerto final. Nesse acerto, a despesa (D) pode ser escrita por D = 55x. No acerto inicial, cada uma das 50 pessoas estava pagando (x - 7) reais e estava faltando 510 reais para completar o valor da despesa, assim D = 50 (x - 7) + 510. Igualando-se às duas equações e realizando a distributiva, tem-se que: 50x – 350 + 510 = 55x.
Logo 5x = 160, x = 32 reais.
d)R$ 32,00.
(ENEM 2004) Em quase todo o Brasil existem restaurantes em que o cliente, após se servir, pesa o prato de comida e paga o valor correspondente, registrado na nota pela balança. Em um restaurante desse tipo, o preço do quilo era R$12,80. Certa vez a funcionária digitou por engano na balança eletrônica o valor R$18,20 e só percebeu o erro algum tempo depois, quando vários clientes já estavam almoçando. Ela fez alguns cálculos e verificou que o erro seria corrigido se o valor incorreto indicado na nota dos clientes fosse multiplicado por:
a) 0,54
b) 0,65
c) 0,70
d) 1,28
e) 1,42
Resolução:
Montando a equação temos
18,20 x = 12,80
x = 0.70
x = 0.70
Logo x=0,70
c) 0,70
c) 0,70
Exercícios Resolvidos Enem Raciocínio Lógico.
RACIOCÍNIO LÓGICO.
Lista de questões resolvidas do ENEM sobre Raciocínio Lógico.
(ENEM 2015) Para uma alimentação saudável, recomenda-se ingerir, em relação ao total de calorias diárias, 60% de carboidratos, 10% de proteínas e 30% de gorduras. Uma nutricionista, para melhorar a visualização dessas porcentagens, quer dispor esses dados em um polígono. Ela pode fazer isso em um triângulo equilátero, um losango, um pentágono regular, um hexágono regular ou um octógono regular, desde que o polígono seja dividido em regiões cujas áreas sejam proporcionais às porcentagens mencionadas. Ela desenhou as seguintes figuras:
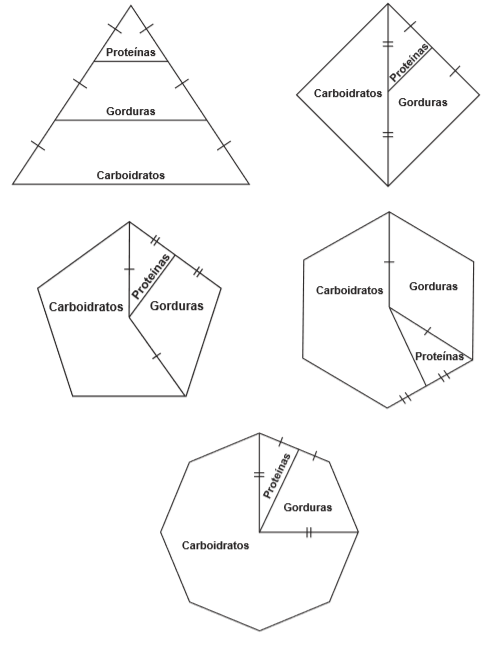
Entre esses polígonos, o único que satisfaz as condições necessárias para representar a ingestão correta de diferentes tipos de alimentos é o
A) triângulo.
B) losango
C) pentágono.
D) hexágono.
E) octógono.
RESOLUÇÃO
A única figura que pode representar as porcentagens citadas é o pentágono.
O pentágono é formado por 5 triângulos.
Se o pentágono todo for 100%, então cada triângulo representa 20%.
Os Carboidratos ocupam três triângulos, logo 3*20% = 60%.
Proteínas ocupam metade de um triângulo, logo 20%/2 = 10%, sobrando 30% para Gorduras.
GABARITO B
(ENEM 2015) Em uma central de atendimento, cem pessoas receberam senhas numeradas de 1 até 100. Uma das senhas é sorteada ao acaso.
Qual é a probabilidade de a senha sorteada ser um número de 1 a 20?
a) 1/100
b) 19/100
c) 20/100
d) 21/100
e) 80/100
RESOLUÇÃO
Probabilidade é: O que queremos / Tudo o que temos.
O que queremos são os números de 1 a 20, logo 20 números.
Tudo o que temos são os números 1 a 100, então temos 100 números no total, assim:
A probabilidade será 20/100.
GABARITO C
(ENEM 2015) No contexto da matemática recreativa, utilizando diversos materiais didáticos para motivar seus alunos, uma professora organizou um jogo com um tipo de baralho modificado. No início do jogo, vira-se uma carta do baralho na mesa e cada jogador recebe em mãos nove cartas. Deseja-se formar pares de cartas, sendo a primeira carta a da mesa e a segunda, uma carta na mão do jogador, que tenha um valor equivalente àquele descrito na carta da mesa. O objetivo do jogo é verificar qual jogador consegue o maior número de pares. Iniciado o jogo, a carta virada na mesa e as cartas da mão de um jogador são como no esquema:
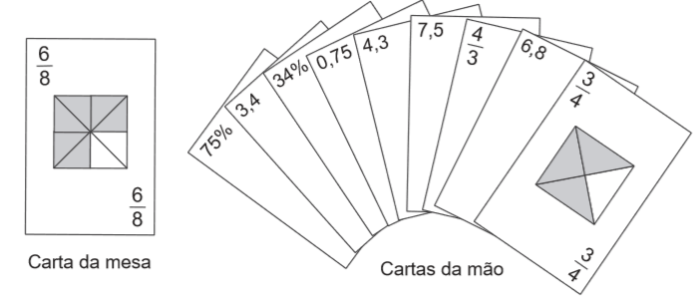
Segundo as regras do jogo, quantas cartas da mão desse jogador podem formar um par com a carta da mesa?
A) 9
B) 7
C) 5
D) 4
E) 3
RESOLUÇÃO
Veja que não temos no baralho nenhuma carta escrita exatamente 6/8, entretanto temos com valores equivalentes.
Simplificando 6/8 temos 3/4, além do mais, 3 dividido por 4 resulta em 0,75 e 0,75 é o mesmo que 75/100 que é o mesmo que 75%.
Logo, temos 3/4; 0,75 e 75%.
GABARITO E.
(ENEM 2015) Após realizar uma pesquisa de mercado, uma operadora de telefonia celular ofereceu aos clientes que utilizavam até 500 ligações ao mês o seguinte plano mensal: um valor fixo de R$ 12,00 para os clientes que fazem até 100 ligações ao mês. Caso o cliente faça mais de 100 ligações, será cobrado um valor adicional de R$ 0,10 por ligação, a partir da 101ª até a 300ª; e caso realize entre 300 e 500 ligações, será cobrado um valor fixo mensal de R$ 32,00.
Com base nos elementos apresentados, o gráfico que melhor representa a relação entre o valor mensal pago nesse plano e o número de ligações feitas é:
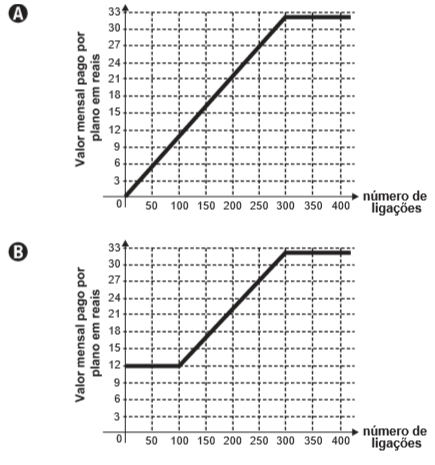
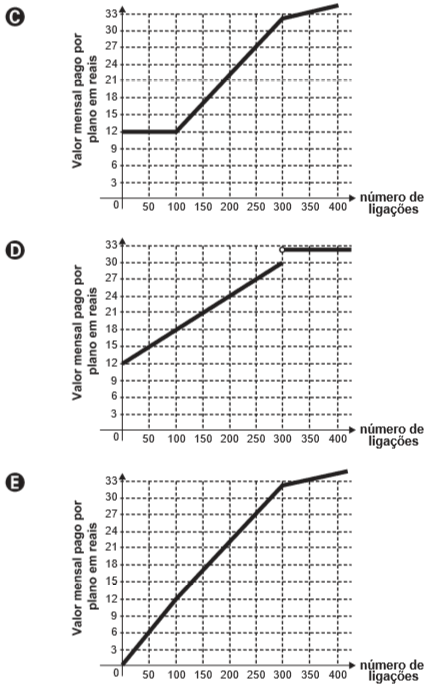
O gráfico certo terá as seguintes informações:
- Valor de R$ 12,00 constante até 100 ligações;
- Valores crescentes até a 300ª;
- Da 300ª até a 500ª o valor será constante de R$ 32,00.
A única alternativa que satisfaz essas condições é B
(ENEM 2015) A insulina é utilizada no tratamento de pacientes com diabetes para o controle glicêmico. Para facilitar sua aplicação, foi desenvolvida uma “caneta” na qual pode ser inserido um refil contendo 3 ml de insulina, como mostra a imagem.

Para controle das aplicações, definiu-se a unidade de insulina como 0,01 mL. Antes de cada aplicação, é necessário descartar 2 unidades de insulina, de forma a retirar possíveis bolhas de ar. A um paciente foram prescritas duas aplicações diárias: 10 unidades de insulina pela manhã e 10 à noite. Qual o número máximo de aplicações por refil que o paciente poderá utilizar com a dosagem prescrita?
A) 25
B) 15
C) 13
D) 12
E) 8
RESOLUÇÃO:
Como antes de cada aplicação deve-se descartar 0,02 ml (2 unidades), então a cada aplicação serão gastos 0,12 ml. Logo, o número máximo de aplicações será:
3 / 0,12 = 25 aplicações.
GABARITO A.
Assinar:
Comentários (Atom)




